En este post vamos a hablar del coeficiente de seguridad en pilares y de si resulta de fiar o hay que tener en cuenta ciertas consideraciones.
La consultoría de estructuras se tropieza todos los días con errores propios y ajenos. Es curioso que, más veces de las que parece, errores y aprendizaje ocurren en la misma obra; es porque los errores nos hacen aprender, eso hace que los errores sean muy educativos y, en el fondo, emocionantes.
En esa misma línea postulamos que el futuro de la ingeniería estructural y de la ingeniería civil en general está en comunicar, en compartir dudas, aciertos, errores, respuestas,… Como queda demostrado en el increíble crecimiento de la computación que tiene su raíz en compartir, programar en abierto, generar comunidad.
Por todo esto, siempre que José Antonio y David me invitan a escribir, intento contaros algún problema, allí donde nuestro equipo de ingenieros aprendió.
Esto nos pasó
Tenemos que revisar una estructura construida hace diez años para absorber un aumento de cargas.
Al cabo de unos días:
- JC ¡tenemos un problema!, el coeficiente de seguridad de varios pilares es 0,2.
- Imposible
- Lo he repasado tres veces y el número es correcto. Hemos usado el prontuario informático del hormigón.
- Me la juego a que no puede ser. Con ese coeficiente, el pilar estaría en el suelo.
Cuando eso pasa, cuando el sentido ingenieril lleva la contraria a los números hay que ser tozudos y buscar. Estuvimos repasando todos los números y estaba todo bien:
- El valor de la fck a partir de testigos
- Los ailes y momentos del pilar para las cargas del proyecto existente
- Y la comprobación del esfuerzo resistente de la sección.
- Y efectivamente salía 0,2…
Así que, como muchas otras veces en la oficina, nos pusimos a criticar todas las expresiones y coeficientes que pudimos a ver si encontrábamos la paradoja.
[Warning:
No es habitual hacer una apropiada valoración de la fck a partir de testigos:
- ¿Cuantos testigos se hacen?
- ¿Cual es el factor aplicable para obtener la característica?
- ¿Qué coeficiente de seguridad se aplican a los materiales?
- ¿y a las acciones?
Hasta hace poco se han venido utilizando métodos semiprobabilistas, poco certeros. El método más apropiado es el método probabilista.
¿Cómo se hace bien? Pocos técnicos lo saben hacer bien]
Repaso de flexocompresiión recta
La flexión simple depende solo de un valor, el del momento. En estos casos se compara una sola variable, M y por tanto la decisión es evidente
- Si Mu = 30
- Md = 28, perfecto
- Md = 20, derroche
- Md = 32, más perfecto aún

- Md = 35, mal
- Md = 60, retirada del carné
Pero, en pilares, los esfuerzos son dos y concomitantes (N, M). En este caso la comparación de esfuerzos resistentes vs. solicitantes es mucho más compleja.
Veamos un ejemplo: Si la pareja (N, M) = (1250, 400) es estrictamente resistida por la sección A, ¿podemos afirmar …
- que si ambos esfuerzo son menores (N, M) = (1200, 300) la situación es segura? parece que sí… pero no se puede afirmar
- que si ambos esfuerzo son mayores (N, M) = (1550, 450) la situación se insegura? parece que sí…pero no se puede afirmar
Cuando hay dos variables el conjunto de parejas de rotura estricta, en hormigón armado, delimitan una línea denominada Diagrama de interacción. Si la pareja solicitante está dentro del diagrama, la sección resiste, y si la pareja solicitante está fuera, no resiste.
Los diagramas de interacción del hormigón tienen esta pinta.
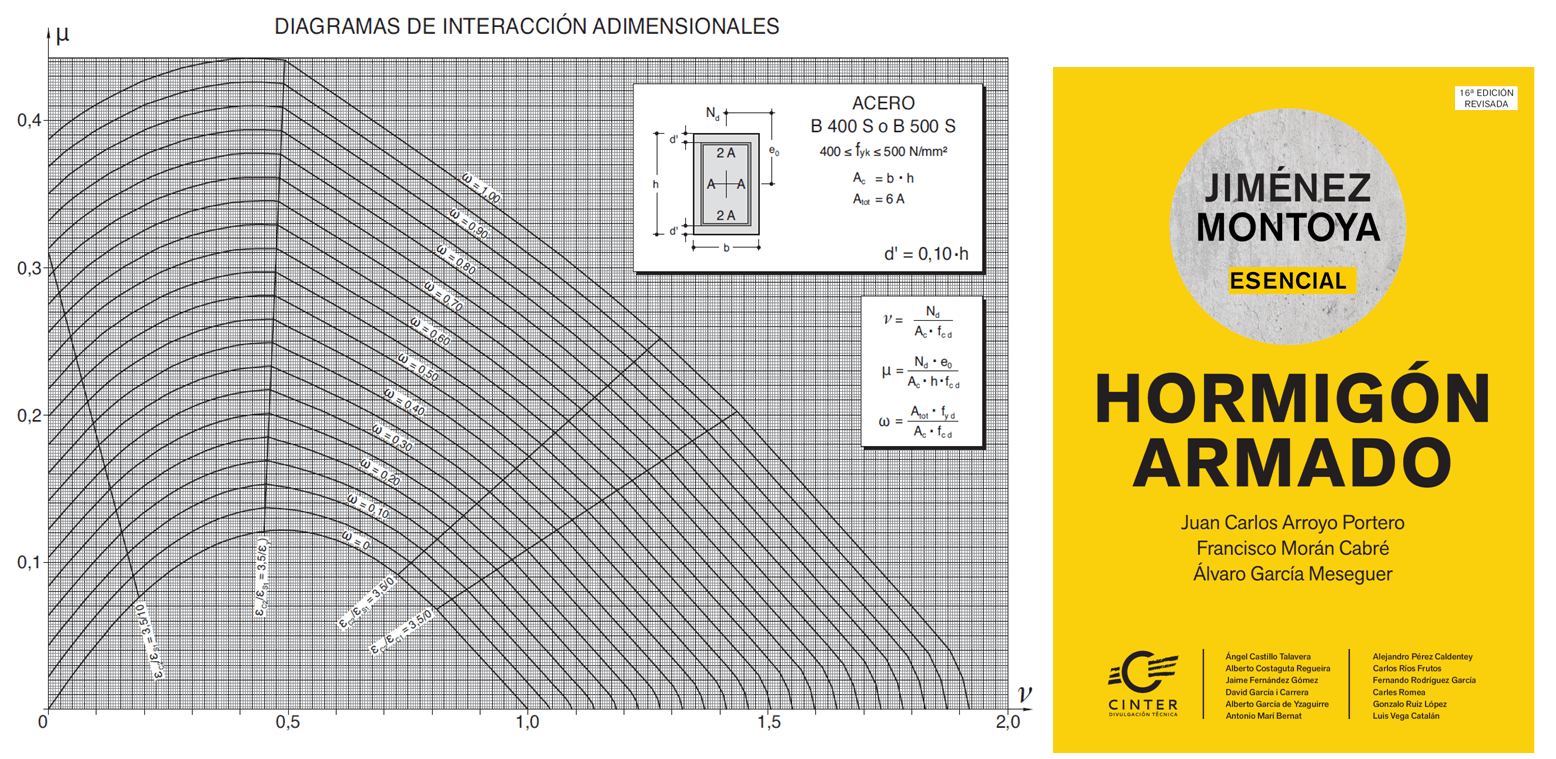
Figura 1: Ábaco extraído del libro de hormigón Jiménez Montoya. (16ª ed, con Ed: CINTER divulgación técnica).
La paradoja de que la pareja de valores menores puede romper la sección lo explica el hecho de que el diagrama de interacción tiene una zona creciente.

Figura 2: Zona creciente del diagrama de interacción.
Este hecho hace difícil la comparación pues no vale con un “mayor que”. Lo más habitual (también en los softwares) es trazar la línea que pasa por el origen y por la pareja en cuestión (1) y calcular el punto del diagrama que intersecta esa recta (1’). O, lo que es lo mismo, calcular qué pareja de rotura tiene la misma excentricidad.

Figura 3: Diagrama de interacción: Criterio de “la recta que pasa por el origen”.
Con este criterio (figura 3), el coeficiente de seguridad es el cociente O1 / O1’. Las pareja (N1, M1) y (N3, M3) son seguras, y la pareja (N2, M2) es insegura.
Esta valoración tiene mucha lógica matemática. Pero si pensamos en el significado físico de mantener constante la relación M/N esto puede suponer, por ejemplo, que crezcan de la misma forma el viento de un hospital (momento) y el número de pacientes (axil).
Existen otras definiciones de coef de seguridad (figura 4, suponiendo que se mantiene el axil constante y solo crece el momento o viceversa.

Figura 4: Diagrama de interacción: Criterio de recta que pasa por el origen (1), criterio de axil constante (2) y criterio de momento constante (3).
Con estas posibles definiciones de seguridad se pueden obtener coeficientes de seguridad muy dispares. Podéis ver (figura 4) que en la pareja A, la seguridad es parecida sea cual sea el método, 1, 2 ó 3. Sin embargo en la pareja B, podéis ver que la seguridad para axil constante es muy pequeña N2 / NB, puesto que NB es varias veces mayor que N2.
En mi opinión, el mejor coeficiente, el más claro, el que mejor idea da de qué nivel de seguridad tenemos es el de la recta que pasa por el origen. De alguna forma lo que medimos es la distancia entre la pareja de esfuerzos solicitantes y el diagrama de interacción.
Repaso de flexocompresión esviada
El caso se complica cuando hay dos momentos, N, Mx y My. siendo, además, mucho más habitual que el de un solo momento.
En ese caso, en lugar de diagrama de interacción (N, M existe una superficie de interacción (N, Mx, My) con la pinta del gráfico siguiente.

Figura 5: Ábaco de roseta para una sección sometida a flexión en dos direcciones.
Estos gráficos son como planos acotados de la superficie de interacción, y representan los cortes de la superficie de interacción con planos de axil constante (figura 6).

Figura 6: Construcción del ábaco de roseta a partir de la superficie de interacción
Con esta construcción estamos aplicando el criterio del axil constante y, como hemos visto, puede dar lugar a valores desproporcionadamente pequeños de la seguridad para axiles cercanos al máximo (Punto 2 de la figura 7).

Figura 7: Dos criterios de obtención de la seguridad en una pareja A (N, Mx, My ) con un axil cercano al máximo.
Por desgracia, muchos programas de cálculo siguen este criterio; daos por avisados.
¿Qué pasó con aquel pilar?
El axil de ese pilar, efectivamente, era cercano al máximo por lo que el coeficiente obtenido era a nuestro juicio, demasiado pequeño.
El objetivo siguiente fue determinar el coeficiente de seguridad dado por el criterio “recta que pasa por el origen”. Así, el asunto se reduce a un problema geométrico de determinación de la distancia de un punto a una superficie.
Lo que se nos ocurrió en Calter fue, utilizando el mismo software, iterar de forma sencilla calculando varios coeficientes de seguridad de forma escalonada como indica el siguiente gráfico.
fuimos consiguiendo los sucesivos coeficientes del trío en cuestión y sus proporcionales (x Ki) hasta encontrar una pareja cuyo coeficiente sea 1 o muy cercano. En coeficiente de seguridad buscado es Ki.
El pilar de esta historia no se salvó pero pasó de tener un coeficiente de seguridad de 0,2, con un refuerzo casi inabordable, a tener un coeficiente de 0,85, fácilmente reforzable.
¿Quieres ser el primero en leer nuestros artículos?
Déjanos tu nombre y un email válido, y nosotros te avisaremos cuando hayan novedades en Estructurando
 |
La entrada ¿El coeficiente de seguridad en pilares es de fiar? aparece primero en Estructurando.
Ver Fuente






Publicar un comentario